上海2017-2018学年第一学期初三期末模拟数学考试试题
1、选择题：（本大题共6题，每题4分，满分24分）
1．在
中，
，
，
，那样
的值是（ ）
； 
； 
； 
．
2．抛物线的顶点坐标是（ ）
； 
； ； 
．
3．在Rt△ABC中，∠C = 90º，AB = 4，AC = 1，那样∠B的余弦值为
（A）
； （B）
； （C）
； （D）
．
4．在△ABC中，点D、E分别在AB、AC的延长线上，下列不可以断定DE//BC的
条件是
（A）
； （B）；
（C）
； （D）
．[来源:学.科.网]
5．假如两圆的半径分别为2和5，圆心距为3，那样这两个圆的地方关系是（）
外离； 外切； 相交； 内切．
6．已知抛物线
:
，将抛物线平移得到抛物线
，假如两条抛物线，
关于直线对称，那样下列说法正确的是
（A）将抛物线沿
轴向右平移
个单位得到抛物线；
（B）将抛物线沿轴向右平移个单位得到抛物线；
（C）将抛物线沿轴向右平移个单位得到抛物线；
（D）将抛物线沿轴向右平移
个单位得到抛物线．
7.如图，在△ABC中，已知∠B和∠C的平分线相交于点F，过Ｆ作DE∥BC，交AB于点D，交AC于点E，若BD+CE=9，则线段DE的长为（ ）.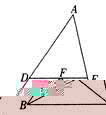
A．9 | B．8 | C．7 | D．6 |
8．下列命题中正确的个数是
① 直角三角形的两条直角边长分别是6和8，那样它的外接圆半径为；
② 假如两个直径为10厘米和6厘米的圆，圆心距为16厘米，那样两圆外切；
③ 过三点可以确定一个圆；
④ 两圆的公共弦垂直平分连心线．
（A）0个； （B）4个； （C）2个； （D）3个．
9.如图，在平行四边形ABCD中，点E在边DC上，DE
：EC=3：
1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（ ）
A．3：4 B．9：
16 C．9：
1 D．3：
1
10.如图所示，已知二次函数y=ax2+bx+c（a≠0）的图象的顶点P的横坐标是4，图象交x轴于点A（m，0）和点B，且m＞4，那样AB的长是（）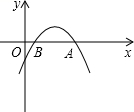
A. 4+m B. m C. 2m-8 D. 8-2m
2、填空题：（本大题共12题，每题4分，满分48分）
11．已知
，那样
______________________________．
12．计算：______________________________．
13．假如一幅地图的比率尺为
，那样实质距离是
km的两
地在地图上的图距是
______________________________cm．
14．假如抛物线有最高点，那样a的取值范围是________________________________________．
15．抛物线
向左平移2个单位长度，得到新抛物线的表达式为________________________________________．
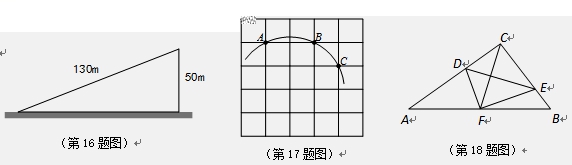
16．如图，一个斜坡长
m，坡顶离水平地面的距离为m，那样这个斜坡的坡度为__________________________________________________．
17．如图，在
正方形网格中，一条圆弧经过A，B，C三点，已知点A的坐标是
，点
C的坐标是，那样这条圆弧所在圆的圆心坐标是______________________________．
18．如图，在中，
，点D, E分别在
上，且
，将
沿DE折叠，点C恰好落在AB边上的点F处，假如，，那样CD的长为______________________________．[来源:学+科+网Z+X+X+K]
19．抛物线
上部分点的横坐标，纵坐标y的对应值如下表：
| … | －3 | －2 | －1 | 0 | 1 | … |
| … | －6 | 0 | 4 | 6 | 6 | … |
容易看出，（－2，0）是它与轴的一个交点，那样它与
轴的另一个交点的坐标为______________________________．
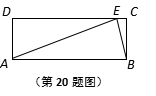
20．如图，矩形ABCD中，点E在边DC上，且AD = 8，[来源:学#科#网Z#X#X#K]
AB = AE = 17，那样______________________________．
21．已知在直角坐标平面内，以点P（1，2）为圆心，r为半
径画圆，⊙P与坐标轴恰好有三个交点，那样r的取值是______________________________．
22．半径分别为20cm与15cm的⊙O1与⊙O2相交于A、B两点，假如公共弦AB的长
为24cm，那样圆心距O1O2的长为________________________________________cm
3、解答卷：（本大题共7题，满分78分）
23．（本题满分10分）
计算：
24．（本题满分10分，每小题各5分）
如图，在中，BE平分
交AC于点E，过点E作
交AB于点D，
已知，
．
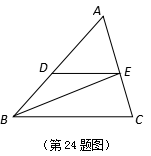（1）求BC的长度；
（2）假如，，那样请用
、表示向量
．
[来源:Z+xx+k.Com]
25．（本题满分10分，每小题各5分）
如图，CD为⊙O的直径，，垂足为点F，
，垂足为点E，
．
（1）求AB的长；
（2）求⊙O的半径．
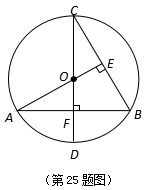
26．（本题满分10分）
如图，港口B坐落于港口A的南偏东
方向，灯塔C恰好在AB的中点处，一艘海轮坐落于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行km，到达E处，测得灯塔C在北偏东方向上．这个时候，E处距离港口A有多远？
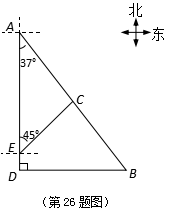（参考数据：
）
27．（本题共2小题，每小题6分，满分12分）
如图，已知在△ABC中，∠BAC =2∠B，AD平分∠BAC，
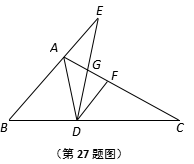DF//BE，点E在线段BA的延长线上，联结DE，交AC于点G，且∠E =∠C．
（1）求证：；
（2）求证：．
28．（本题共3题，每小题4分，满分12分）
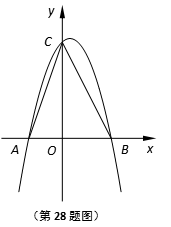抛物线经过点A（，0），B（，0），
且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对
称轴的右边，点E在线段AC上，且DE⊥AC，
当△DCE与△AOC相似时，求点D的坐标．[来源:Zxxk.Com]
29．（本题共3小题，第（1）小题4分，第（2）小题6分，第（3）小题4分，满分14分）
如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，CD是斜边上中线，点E在边AC上，点F在边BC上，且∠EDA=∠FDB，联结EF、DC交于点G．
（1）当∠EDF=90°时，求AE的长；
（2）CE = x，CF = y，求y关于x的函数关系式，并指出x的取值范围；
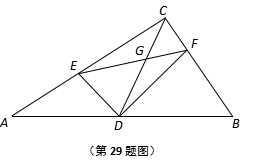
（3）假如△CFG是等腰三角形，求CF与CE的比值．
